သင်္ချာ အတွေးအခေါ် (၂)

သင်္ချာဟာ အတွက်အချက်သီးသန့် မဟုတ်၊ မှန်ကန်တဲ့ တွေးခေါ်မှုပေါ် အခြေခံရတယ်ဆိုတာ အပိုင်း (၁) မှာ ပြောပြခဲ့ပြီးပါပြီ။ “သင်္ချာဟာ သိပ္ပံပညာရဲ့ ဘာသာစကား – Mathematics is the language of Science” လို့ ပညာရှင်တွေ တင်စားကြတယ်။ သင်္ချာကို အတွေးအခေါ်နဲ့ ရောယှက်လိုက်တဲ့အခါမှာ သေးငယ်တဲ့ စက္ကူချပ်လေးကနေ… ကြီးမားတဲ့ စကြဝဠာအထိပါ လက်တွေ့ဆန်ဆန် စိတ်ကူးယဉ်လို့ ရပါတယ်။

ဆိုလိုတာက ကျွန်တော်တို့ လက်လှမ်းမီတဲ့ အချက်အလက်တွေပေါ် အခြေခံပြီး ကျွန်တော်တို့ လက်လှမ်းမမီနိုင်တဲ့ အရာတွေကို တွက်ချက်ကြည့်ခြင်း ပါပဲ။ ဒီအချက်ကို ဘီစီ ၂၄၀ လောက်မှာ သက်သေပြခဲ့သူက အီရာတော့စ်သနီးစ် (Eratosthenes) ဆိုတဲ့ ဂရိစွယ်စုံပညာရှင်ပဲ ဖြစ်ပါတယ်။ သူဟာ ကမ္ဘာရဲ့ စက်ဝန်း (Circumference) ကို ပထမဆုံး တွက်ချက်ပြခဲ့တဲ့ ပညာရှင်ဖြစ်ပါတယ်။

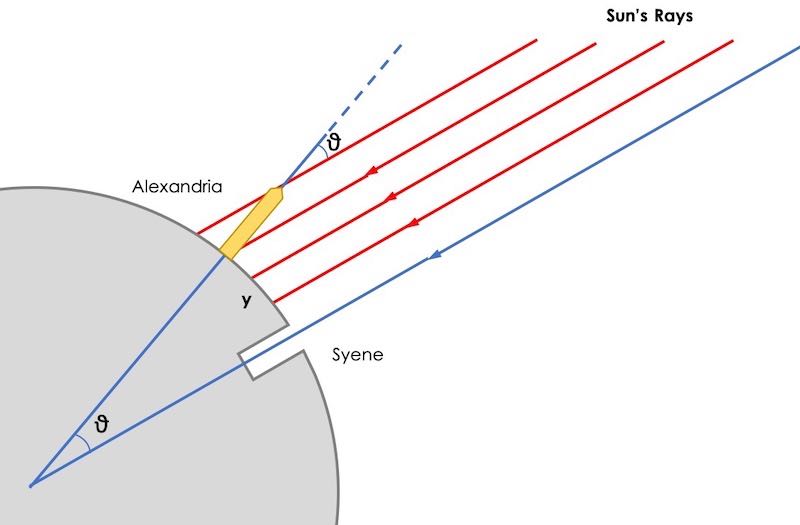
အီရာတော့စ်သနီးစ် နေတဲ့ အလက်ဇန်းဒရီးယား (Alexandria) မြို့ကနေ ကီလိုမီတာ ၈၀၀ ဝေးတဲ့ ဆိုင်ယီးနီး (Syene) မြို့မှာ ရေတွင်းတစ်တွင်း ရှိပါတယ်။ အဲဒီ ဆိုင်ယီးနီးမြို့ဟာ မြောက်လတ္တီကျု ၂၃.၅° ပေါ်မှာ တနည်းဆိုရရင် ဥတ္တရယဉ်စွန်းတန်း (Tropic of Cancer) ပေါ်မှာ ရှိပါတယ်။ ဒါကို သူက ဘာနဲ့အတည်ပြုသလဲဆိုတော့ နွေယဉ်စွန်းချိန် (Summer Solstice) ဇွန်လအလယ်ပိုင်းနေ့တစ်နေ့ နေမွန်းတည့်ချိန်မှာ ဆိုင်ယီးနီးမြို့မှာ ရှိတဲ့ ရေတွင်းတစ်တွင်းဟာ ရေတွင်းနံရံတွေရဲ့ အရိပ်ကျခြင်း မရှိပါဘူး ဆိုတဲ့အချက်နဲ့ပါ။

အဲဒီနေ့ တစ်ချိန်တည်းမှာပဲ ကီလိုမီတာ ၈၀၀ ဝေးတဲ့ အလက်ဇန်းဒရီးယား မြို့မှာရှိတဲ့ ကျေုာက်တိုင်ကြီးမှာတော့ အရိပ်ကျပါသတဲ့။ အရိပ်က ဖြစ်စေတဲ့ ထောင့်ချိုးက ၇.၂° ဖြစ်ပါသတဲ့။ (ပုံမှာ ကြည့်ပါ) ကမ္ဘာမြေပေါ်ကျတဲ့ နေရောင်ခြည်ရဲ့ အလင်းတန်းတွေက အပြိုင်ဖြစ်တာကြောင့် ဝိသမသတ်ထောင့် ဖြစ်ပြီး အဆိုပါ မြို့နှစ်မြို့ကို ဆက်ထားတဲ့ ကမ္ဘာ့စက်ဝန်းစိတ်ကို ခံဆောင်ထားတဲ့ ထောင့်ဟာလည်း ၇.၂° ဖြစ်တယ်လို့ သူက ယူလိုက်ပါတယ်။ ဒီတော့…

၈၀၀ ကီလိုမီတာ / ၇.၂° = ကမ္ဘာ့စက်ဝန်း / ၃၆၀°

ဆိုပြီးအချိုးချလိုက်တာကနေ ကမ္ဘာ့စက်ဝန်းဟာ ကီလိုမီတာ ၄၀၀၀၀ (လေးသောင်း) ဆိုပြီး ရလာပါတယ်။ ဒီနေ့ခေတ် တိုင်းတာမှုအရ ကမ္ဘာ့ရဲ့စက်ဝန်းဟာ အီကွေတာကနေ ယူရင် ၄၀၀၇၅.၀၁ရ ကီလိုမီတာ ဖြစ်ပြီး လောင်ဂျီကျုတွေအတိုင်း ယူရင်တော့ ၄၀၀၀၇.၈၆ ကီလိုမီတာ ဖြစ်တာကြောင့် အီရာတော့စ်သနီးစ်ရဲ့ တွက်ချက်မှုဟာ အတော်လေး နီးစပ်တယ်လို့ ကောက်ချက်ချနိုင်ပါတယ်။ ဒါကတော့ သေးငယ်တဲ့ အစိတ်အပိုင်းလေးကို အခြေခံပြီး ကြီးမားတဲ့ အရာတွေကို သင်္ချာပညာနဲ့ ခန့်မှန်းခြင်းပါပဲ။

အခြားတစ်ဖက်မှာ အင်မတန်ကြီးမားတဲ့ ကိန်းဂဏန်းတွေကို သင်္ချာနဲ့ တွက်ချက်စိတ်ဖြာပြီး နားလည်လွယ်တဲ့အဖြေတွေ ရလာသည် အထိ အသုံးချနိုင်ပါတယ်။ စိတ်ကူးယဉ် ဥပမာတစ်ခု စဉ်းစားကြည့်ရအောင်ဗျာ။ စာဖတ်သူဟာ နေပြည်တော်က ၆ လမ်းသွား ကားလမ်းမကြီးကို ဖြတ်ကူးမလို့ လုပ်နေတယ်ပေါ့။ အနားမှာ မျဉ်းကျားကလည်း မရှိဘူး။ ဒီတော့ ရုတ်တရက် ဖြတ်ပြေးရင် လွတ်ပါ့မလားလို့ စဉ်းစားမိရင် အောက်ပါအတိုင်း တွက်ကြည့်ပါ။

၆ လမ်းသွား ဟိုင်းဝေးလမ်းမကြီးဟာ (လမ်းလယ်ကျွန်းမပါရင်) ခန့်မှန်းခြေ ပေ ၁၂၀ လောက် ကျယ်ပါတယ်။ ဟိုင်းဝေးလမ်းမတွေမှာ ကားတွေဟာ ပျမ်းမျှတစ်နာရီ မိုင် ၅၀ သွားတယ်လို့ယူဆလိုက်ပါ။ (Speed Limit က 60mph ပါ)။ မိုင် ၅၀ ကို ပေဖွဲ့လိုက်ရင် ၂၆၄၀၀၀ (၅၂၈၀ x ၅၀) ပေ ရပါမယ်။ တစ်နာရီဟာ စက္ကန့် ၃၆၀၀ ပါ။ ဒီတော့ ၃၆၀၀ စက္ကန့်ကို ၂၆၄၀၀၀ ပေ သွားတယ်လို့ရပါမယ်။ ဒီတော့ တစ်စက္ကန့်ကို ၇၃.၃၃၃၃ (၂၆၄၀၀၀ / ၃၆၀၀) ပေ ရပါတယ်။

တွေးကြည့်ပါ။ ပေ ၁၂၀ ကျယ်တဲ့ လမ်းမကို စာဖတ်သူ ပြေးမယ်ဆိုရင် ၄ စက္ကန့်လောက် ကြာပါမယ်။ လမ်းတစ်ဝက် အထိ ဆို ၂ စက္ကန့်လောက် ကြာပါမယ်။ မိုင် ၅၀ သွားနေတဲ့ ကားဟာ အရှိန်မလျှော့ဘဲ ဆက်သွားမယ်ဆိုရင် ၂ စက္ကန့်မှာ ၁၄၆ ပေ နီးပါး ရောက်ပါတယ်။ ပုံမှန်လူတစ်ယောက်ဟာ ကားတစ်စီးမောင်းလာတာကို ပေ ၁၀၀ လောက်မှသာ ကောင်းကောင်း မြင်နိုင်တယ်လို့ ဆိုပါတယ်။ ဒီတော့ ၂ စက္ကန့်အတွင်းမှာ စာဖတ်သူက သေချာမစဉ်းစားဘဲ ပြေးကူးလိုက်မယ်ဆိုရင်… ကားကလည်း မူလတစ်နာရီ မိုင် ၅၀ အရှိန်ကို မလျှော့ရင် စာဖတ်သူကို တိုက်သွားပါပြီ။

မှန်ကန်တဲ့ အတွေးအခေါ်သာ အခြေခံရင် သင်္ချာဟာ သေးငယ်တဲ့ အချက်ကနေ ကြီးမားတဲ့အရာကို ပုံဖော်တွက်ထုတ်နိုင်သလို ကြီးမားတဲ့ အရာကနေ သေးငယ်တဲ့ (ကျွန်တော်တို့ နားလည်လွယ်တဲ့) အချက်တွေအထိ ပြန်လည် ပုံဖော်နိုင်ပါတယ်။ နောက်ထပ် နမူနာ တစ်ခုတွေးကြည့်ရအောင်ဗျာ အီရာတော့စ်သနီးစ်က ကမ္ဘာ့စက်ဝန်းကို တိုင်းတာပြတယ်။ ကျွန်တော်တို့က သူ့ရဲ့ ပြောင်းပြန်တွေးကြည့်ရအောင်။ ဒီလိုဗျာ… စာဖတ်သူဟာ ခု ကျွန်တော်ရေးတဲ့စာကို တစ်နေရာတည်းမှာပဲ ငြိမ်ငြိမ်လေး ထိုင်ပြီး ဖတ်နေတယ်လို့ ထင်ပါသလား။

တွေးကြည့်ဗျာ။ ကမ္ဘာဟာ မိမိဝင်ရိုးပေါ်မှာ ၂၄ နာရီကို တစ်ပတ်ပတ်တယ်လို့ ကျွန်တော်တို့ သိကြပါတယ်။ တစ်ပတ်ဆိုတာ အီကွေတာကနေတိုင်းတဲ့ ကမ္ဘာ့စက်ဝန်း ဖြစ်ပြီး ၂၄၉၀၁ မိုင် (ကီလိုမီတာ ၄ သောင်းနီးပါး) ဖြစ်ပါတယ်။ ဒီတော့ တစ်နာရီမှာ ကမ္ဘာဟာ ၁၀၃၇ မိုင် (၂၄၉၀၁/၂၄) နီးပါးလည်ပါတယ်။ တစ်နာရီဟာ ၃၆၀၀ စက္ကန့်ပါ။ ဒီတော့ တစ်စက္ကန့်ကို ၀.၂၈၈ မိုင်… ပေနဲ့ ဆိုရင် ၁၅၂၁ ပေနီးပါး သွားပါတယ်။ ကဲ… လက်တစ်ဖျစ်တီးဆိုတဲ့ တစ်စက္ကန့် အချိန််လေးမှာ စာဖတ်သူဟာ ပေ ၁၅၀၀ ကျော် ခရီးသွားနေပါတယ်နော်။ ဒါတောင် ကမ္ဘာက နေကိုပတ်ပြီးသွားတဲ့ အကွာအဝေးကို ကျွန်တော်တို့ ထည့်တွက်မထားသေးပါဘူး။

အာခီမီးဒိစ်က ပြောပါတယ်… “ကျွန်တော့်ကို ရပ်စရာ နေရာရယ် လုံလောက်တဲ့ ကုတ်တံ (Lever) တစ်ခုသာ ပေးရင် ကမ္ဘာကြီးကို နေရာရွှေ့ပစ်နိုင်ပါတယ်” တဲ့။ ဒါ အမှန်ပါပဲ။ စနစ်တကျ၊ ကြောင်းကျိုးခိုင်လုံတဲ့ အတွေးအခေါ်သာ ရှိရင် သင်္ချာဟာ သေချာဖို့ အတွက် သင်ရတဲ့ ပညာရပ်တစ်ခုဆိုတာ ငြင်းမရပါဘူး။ အခြားတစ်ဖက်မှာ သင်္ချာကို အတွေးအခေါ် မပါဘဲ သင်မယ်ဆိုရင် သင်ပေးတဲ့သူရော သင်ယူတဲ့သူပါ ချာတဲ့ သင်ချာ ပညာဖြစ်သွားပါလိမ့်မယ်။

မေတ္တာဖြင့်
ဟန်သစ်ငြိမ်