ဖဲဗေဒင် အကြောင်း သိကောင်းစရာ (၂)

အပိုင်း (၁) မှာ ဖဲဗေဒင်အကြောင်း မိတ်ဆက်နဲ့ သာမန်ဖဲထုပ် တစ်ထုပ်ရဲ့ ထူးခြားချက်တွေကို ပြောခဲ့ပါတယ်။ အဲဒီ ထူးခြားချက်တွေ အနည်းငယ်ကို ထပ်မံ ဖြည့်စွက်ပြောချင်ပါတယ်။ သာမန်ဖဲထုပ်ထဲကနေ ဂျက်၊ ကွင်း၊ ကင်း တွေကို ဖယ်လိုက်ရင်… ၁ ကနေ ၁၀ အထိ ကျန်ပါမယ်။

အပွင့် ၄ မျိုး (စပိတ်၊ ဟတ်၊ ဒိုင်းမွန်း၊ ကလပ်) စတာတွေပါရင် စုစုပေါင်း အချပ် ၄၀ ရှိပါမယ်။ အဲဒီက နံပါတ်တွေ အကုန်ကို ပေါင်းကြည့်ရင်ဖြင့် စုစုပေါင်း ၂၂၀ (၅၅ x ၄) ရတာကို တွေ့ရပါလိမ့်မယ်။ အဲဒီတော့… သာမန် ရက်ထပ်နှစ် မဟုတ်တဲ့ နှစ်တစ်နှစ်ကို ဇန်နဝါရီ ၁ ရက်က စရေတွက်လိုက်ရင်ဖြင့် ၂၂၀ မြောက် ရက်ဟာ သြဂုတ် ၈ ရက် (၈ လ၊ ၈ ရက်) ဖြစ်တာကို တွေ့ရပါလိမ့်မယ်။

အရပ်ရှစ်မျက်နှာ ရှိပါတယ်။ အဋ္ဌလဂ်ခွင်ရှိပါတယ်။ သရောဒယမှာ ဝဂ္ဂစက်ရှိပါတယ်။ ဗုဒ္ဓဘာသာရဲ့ ကျင့်စဉ်အနေနဲ့ မဂ္ဂင်ရှစ်ပါးကို တွေ့ရှိနိုင်ပါတယ်။ လောကဓံရှစ်ပါးရှိပါတယ်။ ယိကျင်းရဲ့ ပါးကွသင်္ကေတ ရှစ်ခုရှိပါတယ်။ အခြားသော ဘာသာတွေမှာလည်း ၈ ဂဏန်းကို ထူးခြားသော ဂဏန်းအဖြစ် သတ်မှတ်ထားတာကို တွေ့နိုင်ပါတယ်။ ဒါကတော့ သာမန်ဖဲထုပ် တစ်ထုပ်နဲ့ ၈ ဂဏန်းရဲ့ ဆက်စပ်မှုပါပဲ။ ၈ ဂဏန်းက ထူးခြားတာထက် အားအားယားယား ဆက်စပ်ဖို့စဉ်းစားနေသူတွေက ပိုထူးခြားပါတယ်။ ထားပါတော့…

ပြီးခဲ့တဲ့ အခေါက်က ဖဲဗေဒင်ကို လေ့လာရာမှာလိုအပ်တဲ့ အဆင့် ၃ဆင့်ကို ပြောပြခဲ့ပါတယ်။ ဒါ့အပြင် အလွယ်မှတ်နည်းအနေနဲ့ `အပျင်းစွဲတဲ့ ဖဲချပ်ကဗျာ´ ဆိုတာကိုလည်း ပြောပြခဲ့ပါတယ်။ ဒီတစ်ခေါက် မှာတော့ အဲဒီ အဆင့် ၃ ဆင့်ထဲက ပထမအဆင့် (အနီ၊ အနက်) ရဲ့ ပေါင်းစပ်ခြင်းကို အသေးစိတ် လေ့လာကြည့်ကြရအောင်။

ဖဲချပ်တွေဟာ လူတွေလိုပါပဲ။ လူတစ်ယောက်ဆီမှာ ထူးခြားချက်၊ ဂုဏ်ဒြပ် တစ်ခုစီ ရှိကြသလို ဖဲတစ်ချပ်ခြင်းမှာ ရှိတဲ့ ဖွင့်ဆိုချက်တွေက မတူကြပါဘူး။ လူ နှစ်ယောက် တွေ့ကြုံ ဆက်ဆံတဲ့အခါ တစ်ဘက်ကလူနဲ့ လိုက်ပြီး ကိုယ်က ကောင်းလို့ တစ်ဘက်က ဆိုးသည့်တိုင် လူမှုဆက်ဆံရေးအရ ခွင့်လွှတ်လိုက်ရတာတွေ၊ နားလည် လက်ခံပေးလိုက်ရတာ မျိုးတွေ ရှိတတ်ပါတယ်။ အဲလိုပါပဲ… ဖဲချပ်တွေ ၂ ချပ် ၃ ချပ် စသည်ဖြင့် ပေါင်းစည်းတဲ့အခါ မူလ အဓိပ္ပာယ် ဖွင့်ဆိုချက်တွေ အပြင် သူနဲ့ နီးစပ်ရာ ကတ်တွေရဲ့ အနေအထားကို လိုက်ပြီး အဓိပ္ပာယ် ပြောင်းလဲ (သို့) ပေါင်းစပ် ဖွင့်ဆို ပေးရတဲ့ အခါတွေ ရှိပါတယ်။

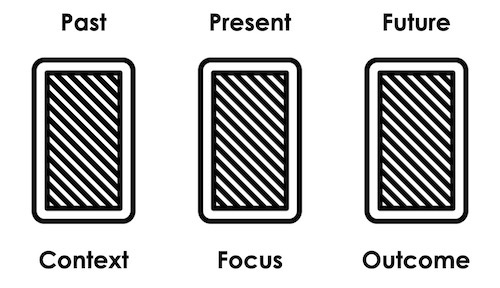
ဒီတော့ ဖဲချပ်တွေကို ပေါင်းစပ်လေ့လာမယ်ဆိုရင် အခြေခံအကျဆုံးဖြစ်တဲ့ အပြင် ရှေး ဂျစ်ပဆီနဲ့ သိုးဆောင်းလူမျိုးတွေ အသုံးပြုလေ့ရှိတဲ့ ၃ ချပ် တွဲနည်းကို လေ့လာခြင်းက အဆင်အပြေဆုံး ဖြစ်ပါတယ်။ ပုံထဲမှာ ပြထားတဲ့ အတိုင်းပါပဲ။ ဘယ်မှညာ ဖဲသုံးချပ်ကို အစဉ်အလိုက်စီပြီး ချလိုက်မယ်ဆိုရင် အတိတ်၊ ပစ္စုပ္ပန်၊ အနာဂတ်ဆိုတဲ့ အစီအစဉ်ကို ရပါမယ်။ တချို့က နောက်ခံအကြောင်းရင်း၊ လက်ရှိဦးတည်ချက်၊ ဖြစ်တည်လာမယ့် ရလာဒ်ဆိုပြီးလည်း ယူဆကြပါသေးတယ်။

ပထမအဆင့် ဥပဒေသအပေါ် အသေးစိတ် လေ့လာခြင်း

ဒီတော့ ဖဲထုပ်ထဲကနေ ကြိုက်တဲ့ ကတ်ပြား ၃ ချပ်ကို လက်တန်းဆွဲထုတ်ပြီး စားပွဲပေါ်ကို ချလိုက်တယ်ဆိုပါတော့… ပထမဆုံး ကတ်ကို ဘယ်ဘက်အစွန်မှာ၊ ဒုတိယကတ်ကို အလယ်မှာ၊ တတိယကတ်ကတော့ ညာအစွန်မှာပေါ့။ အဲဒီအခါမှာ သင်တွေ့ရမှာက အနီနဲ့ အနက်ရောင် ကတ်ပြားတွေရဲ့ ကျရောက်မှုပေါ့… ကျောင်းတုန်းက သင်္ချာကို သင်မမေ့သေးဘူးဆိုရင် ကတ်ပြား ၃ ချပ်နဲ့အတူ အနီနဲ့ အနက်ကျရောက်မှုအရ စုစုပေါင်း ဖြစ်နိုင်ချေ ၈ ခု ရှိတာကို သင်တွေ့ပါလိမ့်မယ်။(၂ သုံးထပ်က ၈ပါ) အဲဒီ ပထမအဆင့် ဖြစ်နိုင်ချေ ၈ မျိုးကို အောက်မှာ ခင်းကျင်းပြထားပါတယ်။ `ပထမဆုံး မှတ်ထားပါ… အနီကောင်းလို့ အနက်ဆိုးတာ´ ဆိုပြီး ပထမ အဆင့်အတွက် ဆိုခဲ့တဲ့ ကဗျာပိုဒ်လေးကို ဒီနေရာမှာ ပြန်သတိရရင်တော့ သုံးချပ်တွဲ အဓိပ္ပာယ်တွေက သင့်အတွက် ခက်ခဲမှာ မဟုတ်ပါဘူး။

နီ – နက် – နက် : 🔴 ⚫️ ⚫️
အစပိုင်း မဆိုးသော်လည်း တဖြည်းဖြည်း အဆိုးဘက်သို့ ပြောင်းလာခြင်း

နက် – နက် – နီ : ⚫️ ⚫️ 🔴
အမှောင်ထဲမှ ထွက်ပေါ်လာသော အလင်းစလေး တစ်စ

နီ – နီ – နက် : 🔴 🔴 ⚫️
ရှေ့လက်တစ်ကမ်းမှာ ပြဿနာကြုံဖို့ ရှိခြင်း

နက် – နီ – နီ : ⚫️ 🔴 🔴
ပြဿနာပြေလည်သွားပြီး အခြေအနေတွေ တိုးတက်လာခြင်း

နီ – နက် – နီ : 🔴 ⚫️ 🔴
ပြဿနာနှင့် နှောင့်နှေးမှု အနည်းငယ် ရှိသော်လည်း ပြေလည်သွားခြင်း

နက် – နီ – နက် : ⚫️ 🔴 ⚫️
ယာယီ သွေးအေးခြင်း၊ ငြိမ်းချမ်းခြင်းမှာ အပေါ်ယံသာဖြစ်ပြီး သတိပြုရမည့် အခြေအနေ ဖြစ်ခြင်း

နီ – နီ – နီ : 🔴 🔴 🔴
အရာအားလုံး အဆင်ပြေချောမွေ့နေခြင်း

နက် – နက် – နက် : ⚫️ ⚫️ ⚫️
ပြဿနာနှင့် အခက်အခဲများ ပြည့်နေခြင်း

ဒီတစ်ခေါက်တော့ ဒီလောက်ပါပဲ။ စာဖတ်သူတို့ ဖင်မနိုင်ပဲ ပဲကြီးဟင်းစားရင် လျှောသွားမှာစိုးရိမ်မိတာ မောင်အုပ်စိုးရဲ့ စေတနာပါ။ တစ်ခုတော့ပြောချင်ပါတယ်။ ကျွန်တော်ပြောပြတဲ့ နည်းစနစ်ဟာ စာအုပ်အတော်များများမှာ ပြောပြတဲ့ နည်းစနစ်မဟုတ်ပါဘူး။ ဒါပေမယ့် လွယ်ကူရိုးရှင်းပြီး လက်တွေ့ကျတာကို အသုံးချတဲ့အခါ သိပါလိမ့်မယ်။

ဘာပဲဖြစ်ဖြစ်ပါ။ တစ်ချပ်တည်း ရပ်တည်နေတဲ့ ဖဲချပ်တစ်ချပ်ဟာ အထီးကျန်ဆန်နေတဲ့ လူတစ်ယောက်လိုပါပဲ။ လှုပ်ရှားမှုမဲ့ အသက်မဲ့နေမှာ အသေအချာပါပဲ။ ဒါကြောင့် ဖဲဗေဒင်ကို လေ့လာမယ်ဆိုရင် တွဲဖက်အဟောတွေကို မေ့ထားလို့ မရပါဘူး။ အဲဒါကို အမြဲတမ်း သတိထားပြီး ဖဲချပ်တွေရဲ့ ပေါင်းစပ်မှုကို လေ့လာကြမယ် ဆိုရင်ဖြင့် ဖဲဗေဒင်ကို အလွယ်တကူ တတ်မြောက်နိုင်မှာ ဖြစ်ပါတယ်။

နောက်ပို့စ်မှာတော့ ဒုတိယအဆင့်ဖြစ်တဲ့ အပွင့် (Suit) တစ်ခုချင်းစီရဲ့ အဓိပ္ပာယ်နဲ့ ဘယ်လို ပေါင်းစပ်ပြီး ဟောရမယ်ဆိုတဲ့ ဥပဒေသကို ပြောပြသွားပါမယ်။

ဆက်ရန်…

အဆင်ပြေမည်ဟု မျှော်လင့် ယုံကြည်လျက်
အုပ်စိုး (mmtl)